Understanding the Surface Area of a Cone: A Simple Guide with a Dash of Humor
Ever seen an ice cream cone? It’s a circle at the bottom and a point at the top. Now, imagine it as a math problem. It might sound scary, but we’re here to make it fun.
What is a Cone?
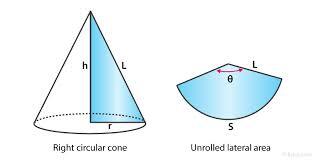
Let’s get to know our cone. Picture it like a party hat or a traffic cone. It has a circular base and a curved surface that points up. It’s like a pizza slice, but without the toppings.
The Components of a Cone
To find a cone’s surface area, we need to know its parts:
- Base: The bottom, a circle. Think of it as the plate your ice cream sits on.
- Slant Height (l): The distance from the base edge to the tip, along the curve. It’s like the length of the cone’s “socks.”
- Height (h): The vertical distance from base to tip. It’s like measuring your cone’s height if it stood up.
Surface Area Formula
To find a cone’s surface area, we calculate two things:
- The area of the base
- The area of the curved surface (also known as the lateral surface area)
Here’s the magic formula:
Surface Area = πr² + πrl
Where:
- π (pi) is about 3.14159 (you might remember it from math classes or pie).
- r is the radius of the base.
- l is the slant height.
Let’s break it down:
- Area of the Base: This is just the area of a circle, which is πr². If you’ve ever found the area of a circle in school, this is the same thing.
- Curved Surface Area: This part is a bit more interesting. To find the area of the curved part, you use πrl. Think of this as wrapping a piece of paper around your cone. If you’re wrapping a gift, this is the part that wraps around the sides.
Putting It All Together
Let’s go through an example. Imagine a cone with:
- A base radius (r) of 3 cm
- A slant height (l) of 5 cm
- Calculate the Area of the Base:Area of the Base = πr²Plug in the values:Area of the Base = π × (3)²Area of the Base = π × 9Area of the Base = 28.27 cm² (approximately, since π is around 3.14159)
- Calculate the Curved Surface Area:Curved Surface Area = πrlPlug in the values:Curved Surface Area = π × 3 × 5Curved Surface Area = π × 15Curved Surface Area = 47.12 cm² (approximately)
- Add Both Areas Together:Surface Area = Area of the Base + Curved Surface AreaSurface Area = 28.27 cm² + 47.12 cm²Surface Area = 75.39 cm²
And there you have it! The surface area of your cone is approximately 75.39 cm².
Why Does This Matter?
Now, you might be wondering, why should I care about the surface area of a cone? It’s useful in many ways:
- Design and Manufacturing: Engineers use these calculations to design things like traffic cones, funnels, and sports equipment.
- Baking and Cooking: If you’re crafting a conical cake or a fancy ice cream cone holder, this math helps you figure out how much frosting or decoration you’ll need.
- Art and Crafting: Artists and crafters use these measurements to create perfect cones for their projects.
Tips and Tricks for Cone Calculations
- Don’t Confuse Height with Slant Height: Remember, the height is straight up and down, while the slant height is along the curved part. They’re like distant cousins—related but not the same.
- Use a Calculator: Pi is a never-ending number, so unless you’re a math wizard with a good memory, it’s best to use a calculator to get the most accurate results.
- Practice: The more you work with these formulas, the easier they become. Like riding a bike, you’ll get the hang of it with a little practice.
Final Thoughts
So there you have it—a simple and somewhat humorous guide to understanding the surface area of a cone. It’s like the math version of enjoying a nice ice cream cone: sweet, satisfying, and a little bit sticky if you’re not careful. Whether you’re designing, baking, or just trying to impress your friends with your newfound math skills, understanding the surface area of a cone is a handy tool to have in your arsenal.
And remember, if you ever find yourself in a cone-related conundrum, just think of this guide, grab your calculator, and you’ll be calculating like a pro. Happy calculating!